《統計業務知識》之：對模糊現象的評價(3)
瀏覽
收藏
二、講解內容 $lesson$
1.主成分分析的基本思路和簡單數學解釋
主成分分析就是把多個指標簡化為少數幾個綜合指標的統計分析方法，它能使這些綜合指標盡可能地反映原來多個指標的信息，并保證這些綜合指標彼此之間互不相關。
主成分分析的數學解釋：
設有p個原始指標：x1,x2,x3,…xp，用來對n個單位進行評價，則共有np個數據。
這p個原始指標之間往往存在著一定的相關性，主成分分析的目的是要將這些原始指標組合成新的不相關的指標：y1,y2,y3,…yp，以使各指標在整個經濟過程中的作用容易解釋，這些綜合指標表現為原始指標的線性函數：
y1=l11x1+l12x2+…l1pxp
y2=l21x1+l22x2+…l2pxp
yp=lp1x1+lp2x2+…lppxp
由于所組合成的新指標：y1,y2,y3,…yp彼此不相關，就使我們有可能從中選擇主要成分，通過對主要成分的重點分析，達到綜合評價的目的。
通過數學計算可以將p個指標的總方差分解為p個不相關的綜合指標的方差之和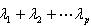
并使第一個綜合指標y1方差達到最大(貢獻率最大)，第二個綜合指標y2的方差次大，依此類推，一般前面幾個綜合指標y1,y2,y3,…yr(r
2.計算步驟
主成分分析可分為以下幾個主要步驟：
(1)列出指標數值矩陣X
(2)計算X的協方差矩陣S。為了消除指標間不同量綱的影響，一般需先對原始數據進行標準化處理，而變換后的標準化值的協方差矩陣恰好是原始指標數值X的相關矩陣。因此，計算協方差矩陣可簡化為計算相關矩陣R。
(3)計算協方差矩陣S(或相關矩陣R)的特征值λ和特征向量L(即指標x的系數)。
(4)計算貢獻率和累計貢獻率，據以確定主成分(即綜合指標)的個數，并建立主成分議程。
每個主成分yk的貢獻率等于它的特征值λk除以原始指標個數p，累計貢獻率等于各主成分貢獻率順序相加，根據一定的選擇標準，如果前r個主成分的累計貢獻率大于或等于80%，(r y1=l11x1+l12x2+…l1pxp y2=l21x1+l22x2+…l2pxp yp=lr1x1+lr2x2+…lrpxp (5)解釋各主成分的意義，并將各單位的原始數據代入方程中計算綜合評價值進行分析比較。在多指標綜合評價中，一般只需取第一個主成分y1作為全面反映各指標狀況的綜合指標，因為它綜合原始指標信息的能力最強。然后，根據這個綜合指標值進行各參評單位的比較評價。
最新資訊
- 統計師真題回顧：2021年初級、中級統計師考試真題及答案解析(附2025年高頻考點)2025-09-22
- 2025年統計師考試備考寶典：近5年統計師考試真題及答案(初級+中級)2025-09-19
- 統計師真題回顧：2023年統計師真題及答案解析(初級+中級)2025-09-17
- 統計師備考資料：2024年統計師真題回顧+2025年高頻考點(初級+中級)2025-09-16
- 2025年初級統計師備考指南：思維導圖+高頻考點(附歷年真題)2025-09-16
- 2025年中級統計師考試備考資料：思維導圖+高頻考點(附歷年真題)2025-09-15
- 統計師備考：2025年統計師高頻考點(初級+中級)2025-08-18
- 統計師備考：2025年統計師思維導圖(初級+中級)2025-08-18
- 2025年初級統計師思維導圖-《統計業務知識》2025-08-18
- 2025年中級統計師思維導圖-《統計業務知識》2025-08-18
打卡人數
