2010注冊結構工程師備考:例題(16)
更新時間:2010-06-23 09:33:30
來源:|0
 瀏覽
瀏覽 收藏
收藏
結構工程師報名、考試、查分時間 免費短信提醒
(三)例題
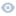
[例4-3-19] 圖4-3-54所示的懸臂梁,在自由端上掛一彈簧,彈簧上懸掛一重P的 物體。設在力P作用下彈簧的靜伸長為δst,梁的自由端的靜撓度為fst。如給重物一初速度v0,試求重物的自由振動方程。梁和彈簧的質量均忽略不計。
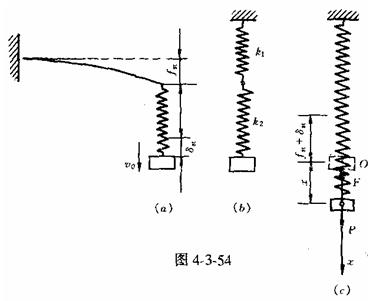
[解] 懸臂梁對物體的作用相當于一彈簧,根據懸臂梁端點的靜撓度fst可算出此梁 在端點沿鉛垂方向的剛性系數為
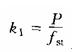
類似地,可算出懸掛彈簧的剛性系數為
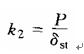
于是,圖4—3—54(a)所示振動系統可以抽象為圖4—3—54(b)所示的串聯彈簧系統。又因串聯彈簧可用一等效彈簧來替代,其當量剛性系數為
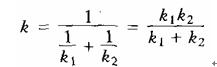
最終該系統可簡化為圖4—3—54(c)所示的質量彈簧系統。現以此力學模型進行求解。
(1)對象。取重物為研究對象。
(2)運動分析:重物由于初始干擾,沿鉛垂方向作自由振動。為了簡便,選取重物的靜平衡位置O為坐標原點,x軸向下為正。t=0時x0=0, 。
(3)受力分析。通常,將重物放在x軸正向的任一位置上進行受力分析。作用其上的力有重力P和彈性力F,力F在x軸上的投影為
![]()
(4)列運動微分方程,并求解振動規律。由F=ma得
![]()
因重物處于靜平衡位置時,重力P與靜變形引起的彈性力F0平衡,即有
![]()
故上式可簡化為
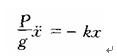
即
![]()
式中
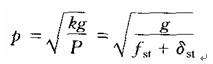
由表4—3—11所示的公式,可知式(3)的通解為
![]()
根據初始條件x0=0, ,可分別求得振幅A及初位相α為
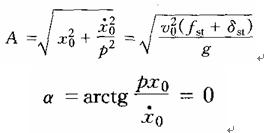
2010年注冊結構工程師考試報名時間信息匯總
結構工程師基礎科目(一)考試普通化學練習題匯總
2010年結構師考試9月18、19日
更多信息請訪問:結構工程師頻道 結構工程師論壇
編輯推薦
最新資訊
- 2025年一級注冊結構工程師考前實戰試題解析:突破考試瓶頸的終極指南‌2025-10-13
- 2025年一級注冊結構工程師常考知識點2025-02-17
- 2025年二級注冊結構工程師高頻知識點2025-02-17
- 2024年度二級注冊結構工程師專業考試資料:規范、標準、規程2024-08-13
- 2024年度一級注冊結構工程師專業考試資料:規范、標準、規程2024-08-13
- 環球網校雙11預售開啟!定金百倍膨脹,直播再返現金2023-10-25
- 環球網校結構工程師雙11活動來啦,限時優惠!2023-10-25
- 注冊結構工程師考試大綱下載2023-05-16
- 2023年一級注冊結構工程師考試大綱內容2023-04-14
- 2023年結構工程師教材內容變動對比2023-04-10
 打卡人數
打卡人數


