09年統計基礎知識統計整理復習資料五
環球網校為使廣大學員更好的備戰2009年統計師考試,為您提供統計師考試資料,這一節主要講的是第三講:統計工作過程及基本方法3.統計分組次數分布復習資料。祝大家2009年統計師考試順利!
(3)組距數列的編制
在編制過程中,要正確處理以下三個具體問題。
①組數與組距
編制組距數列,必須對總體進行分組,針對一個總體,應將其分為多少組,這要根據研究的目的來確定,同時要本著以能簡單明了地反映問題為原則。如果組數過多,必然會造成總體單位分布分散,同時還有可能把屬于同類的單位歸到不同的組中,不能真實反映出事物的本質特點和規律性;如果組數過少,又會造成把不同性質的單位歸到同一個組內,失去區別事物的界限,達不到正確反映客觀事實的目的。因此,必須恰當地確定組數。美國學者斯特奇斯(HASturges)提出,在總體各單位標志值分布趨于正態的情況下,可根據總體單位數(N)來確定應分組數(n),公式為:
n=1+3.322lgN
上式可供分組時參考,但也不能生搬硬套。當總體單位數過少時,按上述公式計算的組數可能偏多;而當總體單位數很多時,計算的組數又可能偏少。
確定組數后,還應確定組距。組數和組距之間存在著密切關系。在全距(最大變量值與最小變量值之差)一定的情況下,組距的大小和標志變量數列的全距大小成正比變化,與組數多少成反比變化。
組數越多,組距越小;組數越少,組距越大。由于組距數列有等距數列與異距數列之分,在采用等距分組的情況下,變量數列編制的組距(d)可采用下列公式確定:

按照斯特奇公式有: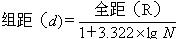 例如:要調查50人的年齡狀況,50人中最高年齡為70歲,最低年齡為3歲,故全距R=70-3=67歲,總次數N=50人,其對數lg50=1.6990,則
例如:要調查50人的年齡狀況,50人中最高年齡為70歲,最低年齡為3歲,故全距R=70-3=67歲,總次數N=50人,其對數lg50=1.6990,則
組距= 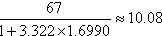 ,組數=67/10 ,即這個次數分布表的組距為10,共有7組數據。
,組數=67/10 ,即這個次數分布表的組距為10,共有7組數據。
②組限與組中值
組距數列中,每個組都有兩個端點,這兩個端點稱為組限。數值小的端點稱為組的下限,數值大的端點稱為組的上限。
若一組內有上限缺下限,或有下限缺上限稱為開口組;
若一組內的上限、下限都齊全稱為閉口組。
組距數列掩蓋了組內各單位的實際變量值,通常用組中值近似地代替每組變量值的一般水平。
組中值=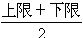 計算開口組的組中值中,
計算開口組的組中值中,
如果只有上限沒有下限:組中值=上限-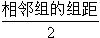 如果只有下限沒有上限:組中值=下限+
如果只有下限沒有上限:組中值=下限+ 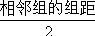 注意:用組中值來代表各組的一般水平時,變量值在該組應呈均勻分布,或在組中值兩側呈對稱分布,否則,用組中值作為一組的代表值會有一定的誤差。
注意:用組中值來代表各組的一般水平時,變量值在該組應呈均勻分布,或在組中值兩側呈對稱分布,否則,用組中值作為一組的代表值會有一定的誤差。
2009年統計師考試相關信息:
最新資訊
- 倒計時5天!2025年統計師考試考前必背考前幾頁紙!(初級+中級)2025-10-14
- 僅剩9天!2025年統計師考試考前沖刺備考資料免費下載(初級+中級)2025-10-10
- 免費下載!沖刺階段的復習寶典-2025年中級統計師考前幾頁紙(各科目匯總)2025-10-10
- 必背資料!2025年中級統計師考試-經濟學基礎知識-考前10頁紙2025-10-10
- 沖刺寶典!2025年中級統計師考試-會計基礎知識-考前12頁紙2025-10-10
- 考前必背!2025年中級統計師-統計學基礎知識-考前14頁紙2025-10-10
- 沖刺必備:2025年中級統計師-統計實務-考前10頁紙2025-10-10
- 統計師考前沖刺:2025年中級統計師-統計法規-考前5頁紙2025-10-10
- 統計師考試倒計時!2025年初級+中級考前幾頁紙關鍵知識點速記2025-10-10
- 免費下載-考前急救!2025年初級統計師考前幾頁紙(匯總)2025-10-09


 打卡人數
打卡人數


