2008年統(tǒng)計工作實務國民經濟復習資料(8)
瀏覽
收藏
(四)投入產出統(tǒng)計
1． 投入產出表的基本表式
投入產出表是行列交織的棋盤式平衡表，其描述對象是一個經濟體系在一定時期內所發(fā)生的投入產出關系。
投入產出表的基本設計原則是：在行的方向表示各部門生產活動的產出及其使用，在列的方向表示各部門生產活動的投入及其來源。行表示產出而列表示投入，這就是投入產出表得名的由來。
根據(jù)產品使用方向之不同，可將產品分為兩大類：中間產品與最終產品。
在投入方向上，投入物也包括兩個部分：中間投入和增加值。
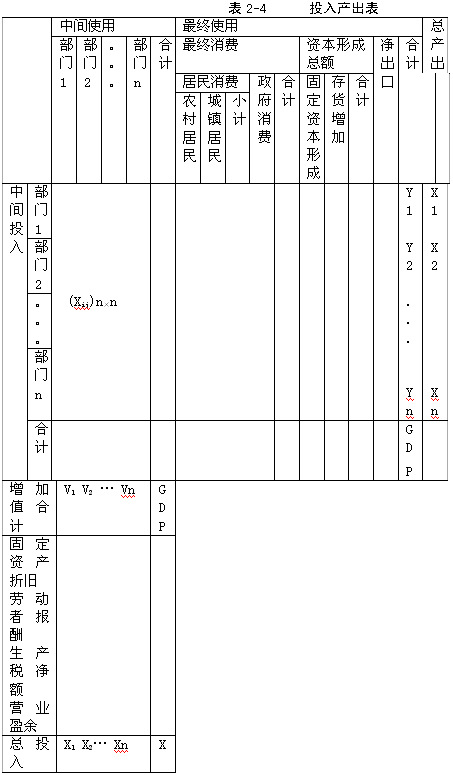
如上表中，假定經濟系統(tǒng)包括n個部門，把上述產出的類別和投入的類別交叉聯(lián)立，就形成投入產出表的四個象限。
第Ⅰ象限是一個n行n 列的矩陣，反映貨物和服務在部門間的流量。在行列交叉處，元素Xij具有雙重含義，一方面它表示當期第j部門在生產過程中對第i部門產品的消耗量，即在j部門生產過程中有Xij數(shù)量的i部門產品作為中商投入被j部門所消耗；另一方面它表示當期i部門產品分配給j部門使用的數(shù)量。通過這個矩陣，就將原來按不同標準分類的中間產品和中間投入整合在一起。第Ⅰ象限是整個投入產出表的核心，充分揭示了國民經濟各部門之間相互依存、相互制約的技術經濟聯(lián)系。
第Ⅱ象限是第Ⅰ象限在行方向上的延伸，Yi表示第i部門產品用作最終產品的數(shù)量。最終產品一般又可分為消費、資本形成和出口，其中前兩項還可以進一步細分。這樣第II象限就表示各部門產品用作各類最終產品的數(shù)量，它也是一個矩陣但一般不是方陣。最終產品與中間產品的合計即為總產品。
第Ⅲ象限為第Ⅰ象限在列方向上的延伸，Vj表示第j部門最初投入。最初投入一般分為：固定資產折舊、勞動者報酬、生產稅凈額和營業(yè)盈余。最初投入與中間投入合計即為總投入。
第Ⅳ象限在理論上反映收入再分配的情況，但由于這一過程難以納入最初投入與最終產品所構成的矩陣框架，所以一般為空項。
1． 投入產出表的基本平衡關系
在投入產出表中有一些基本的總量平衡關系。具體歸納如下：
總投入=總產出
中間投入+增加值=總投入
中間使用+最終使用=總產出
增加值合計=國內生產總值=最終使用合計
需要特別指出的是，在總產出與總投入之間具有平衡關系，不僅一個經濟總體的總投入等于其總產出，而且在單個部門層次上總投入也等于其總產出。
通過對投入產出表進行投入產出分析，可以系統(tǒng)反映產業(yè)之間的關聯(lián)。其基本方法是以第Ⅰ象限為依據(jù)，通過中間投入流量計算各產業(yè)間的直接消耗系數(shù)和完全消耗系數(shù)。
直接消耗系數(shù)又稱為投入系數(shù)或技術系數(shù)，一般用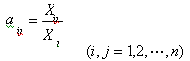
對所有產業(yè)計算直接消耗系數(shù)，結果構成一個系數(shù)矩陣，通常用A表示。直接消耗系數(shù)只反映了產業(yè)間的直接聯(lián)系，卻不能反映產業(yè)間聯(lián)系。需要在直接消耗系數(shù)基礎上計算完全消耗系數(shù)，既反映直接聯(lián)系，也反映間接聯(lián)系。單個完全消耗系數(shù)用b表示，對所有產業(yè)計算完全消耗系數(shù)，所形成的矩陣用B表示，它是依據(jù)直接消耗矩陣計算得到的，其計算公式如下：
B=(I-A)-1-I
式中(I-A)-1稱為列昂惕夫逆矩陣，也是用來分析產業(yè)聯(lián)系的重要工具。
如果用X表示總產出向量，用Y表示最終使用向量，則中間使用矩陣為AX，根據(jù)投入產出表中的平衡關系可以得到：
AX+Y=X
從而有：
(I-A)-1Y=X
把上式寫成差分形式，得到
(I-A)-1 ㄓY=ㄓX
可見列昂惕夫逆矩陣度量了最終使用與總產出之間聯(lián)系的強度，它的含義是，如果每個產業(yè)的最終使用都增加一個單位，則各產業(yè)總產出將增加的單位數(shù)。
［例2-5］根據(jù)表2-5提供的示意性數(shù)據(jù)，計算對應部門的直接消耗系數(shù)。
表2-5 投入產出---示意數(shù)據(jù)
|
|
中間產出 |
最終產品 |
總 產 出 |
| |||||||
|
農業(yè) |
工業(yè) |
其他 |
小計 |
消費 |
投資 |
凈出口 |
小計 |
| |||
|
中 間 投 入 |
農業(yè) 工業(yè) 其他 |
12 17 11 |
25 50 15 |
5 16 2 |
42 83 28 |
25 50 10 |
2 28 7 |
1 -1 -1 |
28 77 16 |
70 160 44 |
|
|
小計 |
40 |
90 |
23 |
153 |
85 |
37 |
-1 |
121 |
274 |
| |
|
最初投入 |
固定資產折舊 凈增加值 |
2 28 |
13 57 |
3 18 |
18 103 |
|
|||||
|
|
|||||||||||
|
小計 |
30 |
70 |
21 |
121 |
|
| |||||
|
總投入 |
70 |
160 |
44 |
274 |
|
| |||||
上表第Ⅰ象限如果用數(shù)學模型表示如下：表中的黑體字是計算直接消耗系數(shù)的數(shù)據(jù)。
直接消耗系數(shù)計算過程轉換表
|
|
中間產出 |
| ||||
|
農業(yè) |
工業(yè) |
其他 |
小計 |
| ||
|
中 間 投 入 |
農業(yè) 工業(yè) 其他 |
12=X11 17=X21 11=X31 |
編輯推薦
最新資訊
統(tǒng)計師歷年真題下載 更多
返回頂部
| |||
打卡人數(shù)
