結構工程師基礎科目(二)輔導:靜定平面桁架(一)
八、靜定平面桁架
(一)理想平面桁架的假定及其按幾何組成的分類。
理想桁架應滿足下面三個假定:1.各結點均為無摩擦的理想鉸;2.各桿件軸線均為 直桿,且各通過鉸的幾何中心;3.荷載都作用在結點上。如圖2―l
符合上述假定的理想桁架的各桿只承受軸向力,橫截面上只產生均勻的法向應力,與梁相比,受力合理,用料經濟,自重較輕,可跨越較大的跨度。
不符合上述假定的桁架,在桿件中會產生彎曲次應力,理論分析和實驗表明,當桁架的桿件比較細長時,這種次應力與由軸力引起的應力相比所占比例不大。
桁架按其幾何組成可分為:
簡單桁架――從僅由三根桿件組成的三角形鉸接單元出發(fā),根據兩元片規(guī)則,逐次擴展形成的桁架,如圖2-
聯合桁架――由兩個或兩個以上的簡單桁架聯合組成的桁架,如圖2-10b所示。
復雜桁架――不屬于上述兩類的桁架,如圖2-
桁架的有關術語表示在圖2-
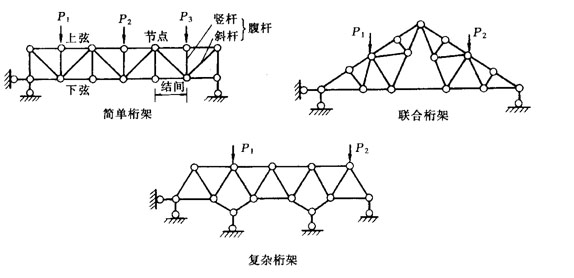
圖2-10
(二)平面桁架的內力計算
1.節(jié)點法
取桁架的節(jié)點為隔離體,由平面匯交力系的平衡條件求解各桿內力的方法。從理論上講,任何靜定平面桁架都可利用節(jié)點法求出全部桿件的內力,但為了避免求解聯立方程,在每次截取的節(jié)點上不應超過兩個未知內力。在簡單桁架中,只要按兩元片規(guī)則,循著各節(jié)點形成的順序或相反的順序,逐次應用節(jié)點法,在每個結點的平衡方程中,最多不會超過兩個未知力。
在計算中,有時可利用下面幾種節(jié)點平衡的特殊情況。
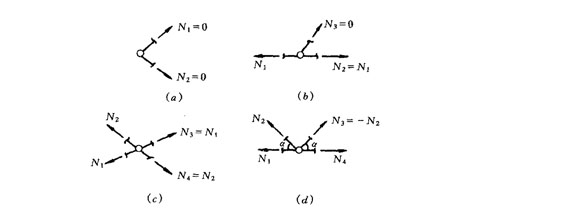
(1)兩桿節(jié)點上無荷載,兩桿內力均為零(圖2―
(2)三桿節(jié)點上無荷載,其中在同一直線上的兩桿內力相等而方向相反,另一桿內力為零(圖2―11b);
(3)四桿節(jié)點上無荷載,且四桿相交成兩直線,則處在同一直線上的兩桿內力相等,但方向相反(圖2―
(4)四桿節(jié)點上無荷載,其中兩桿共線而另兩桿處于此線的同側且傾角相同,則處于共線桿同側的兩桿內力等值而反向(圖2―11d)。
?08年考試規(guī)范、標準: 2008年一級注冊結構工程師考試成績查詢匯總
圖2-11
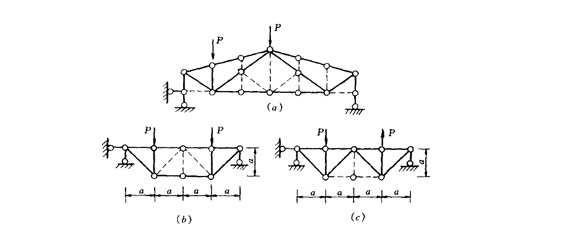
應用上述識別零桿的方法,容易看出圖2―
圖2―12b、c分別為對稱桁架承受對稱荷載和反對稱荷載作用。根據對稱結構在對稱荷載(或反對稱荷載)作用下,其內力為對稱(或反對稱)的特點,再根據上述識別零桿的方法,可知圖中虛線所示的桿件為零桿。
在建立節(jié)點平衡方程時,對于斜桿軸力N,常可用其水平分力X或豎向分力Y作為未知數。再設斜桿長為l,其水平和豎向投影長度分別為lx和ly,則可得
N/l= X/lx =Y/ly (2―9)
由上式可從任一分力X或Y求出軸力N,也可由一個分力算出另一分力,以簡化計算。
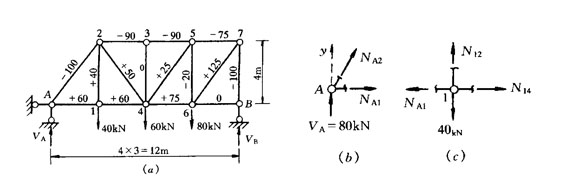
[例2-3] 用節(jié)點法求圖2―
[解]
(1)求支座反力
由整體平衡條件,得VA=80kN,HA=0,VB=100kN。
(2)求桁架各桿軸力
從只含兩個未知力的節(jié)點A(或節(jié)點B)開始,再依次分析鄰近節(jié)點。
節(jié)點A(圖2―13b),設未知軸力為拉力,并采用NA2的水平分力XA2或豎向分力YA2作為未知數,則由
ΣY=0,得YA2=-VA=―80kN
再由式(2―9)得
XA2=-60kN
NA2=―100kN
再由ΣX=0,得NAl=60kN
節(jié)點1(圖2―
依次再考慮節(jié)點2、3、4、5、6、7,每―結點不超過兩個未知力。至最后節(jié)點B時,各桿軸力均為已知,可據此節(jié)點是否滿足平衡條件作為內力計算的校核。各桿軸力計算的結果標注在圖2―
最新資訊
- 2025年一級注冊結構工程師考前實戰(zhàn)試題解析:突破考試瓶頸的終極指南‌2025-10-13
- 2025年一級注冊結構工程師常考知識點2025-02-17
- 2025年二級注冊結構工程師高頻知識點2025-02-17
- 2024年度二級注冊結構工程師專業(yè)考試資料:規(guī)范、標準、規(guī)程2024-08-13
- 2024年度一級注冊結構工程師專業(yè)考試資料:規(guī)范、標準、規(guī)程2024-08-13
- 環(huán)球網校雙11預售開啟!定金百倍膨脹,直播再返現金2023-10-25
- 環(huán)球網校結構工程師雙11活動來啦,限時優(yōu)惠!2023-10-25
- 注冊結構工程師考試大綱下載2023-05-16
- 2023年一級注冊結構工程師考試大綱內容2023-04-14
- 2023年結構工程師教材內容變動對比2023-04-10
 打卡人數
打卡人數


